Heat Conduction in One Dimension

Two metallic blocks $M_1$ and $M_2$ of same area of cross-section are connected to each other (as shown in figure). If the thermal conductivity of $M_2$ is $K$ then the thermal conductivity of $M_1$ will be : [Assume steady state heat conduction]

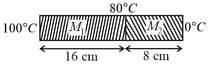
Six identical rods are joined together to form a network as shown. A temperature difference of $\Delta T$ can be maintained between two points. Considering heat flow through conduction only, in steady state :-

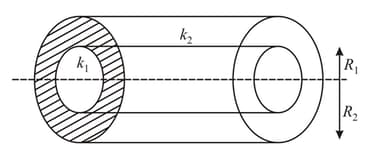
A composite cylinder is made by two materials having thermal conductivities $k_1$ and $k_2$ as shown. Temperature of the two flat faces of cylinder are maintained at $T_1$ and $T_{2.}$

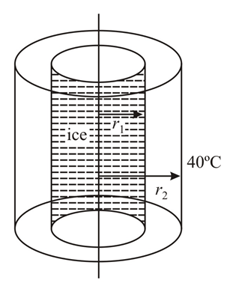
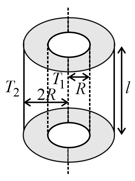
A $100 \mathrm{cm}$ long cylindrical flask with inner and outer diameters $2 \mathrm{cm}$ and $4 \mathrm{cm}$ respectively is completely filled with ice at $0°\mathrm{C}$ as shown in the figure. The constant temperature outside the flask is $40°\mathrm{C}.$ (Thermal conductivity of the flask is $10\ln 2 \mathrm{W} {\mathrm{m}}^{-1}°\mathrm{C},$ Latent heat of friction of ice $\left.{\mathrm{L}}_{\mathrm{ice} }=80\mathrm{cal} {\mathrm{gm}}^{-1},1\mathrm{cal}=4.2 \mathrm{J}\right).$

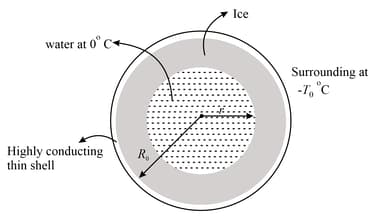
A highly thin conducting spherical shell of radius $R_0$ is completely filled with water at $0°\mathrm{C}$. Outside surrounding temperature is $-T_0{}^{\circ }\mathrm{C}$. Latent heat of fusion of water is $L_0$ and thermal conductivity of ice is $K_{\mathrm{ice}}$. Assume heat is flowing symmetrically in radial direction. Choose the CORRECT option(s). Density of water is ${\rho }_0$. Neglect the expansion of water on freezing.

$1.56\times {10}^5 \mathrm{J}$ of heat is conducted through $2 {\mathrm{m}}^2$ wall of $12 \mathrm{cm}$ thickness in $1 \mathrm{h}$. Temperature difference between the two sides of the wall is $20 °\mathrm{C}$. The thermal conductivity of the material of the wall is (in ${\mathrm{W} \mathrm{m}}^{-1\mathrm{ }}{\mathrm{K}}^{-1}$) $\alpha$. Write the value of $100\alpha$.

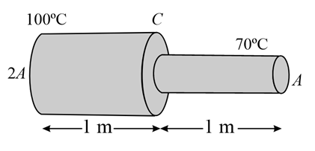
A metal rod of length $2 \mathrm{m}$ has cross sectional areas $2A$ and $A$ as shown in the figure. The ends are maintained at temperatures $100°\mathrm{C}$ and $70°\mathrm{C}$. The temperature at middle point $C$ is___$°\mathrm{C}$.

The end $A$ of a rod $AB$ of length $1 \mathrm{m}$ is maintained at $100 °\mathrm{C}$ and the end $B$at $10 °\mathrm{C}$. What is the temperature (in $°\mathrm{C}$) at a distance of $60 \mathrm{cm}$ from the end $B$?

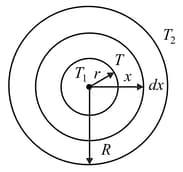
A spherical shell of inner and outer radii $r$and $R$ has variable thermal conductivity $K=\frac{\rho }{x}$, where $k$ is coefficient of thermal conductivity and $x$ is the distance from the centre of spherical shell and $\rho$ is a positive constant. If inner and outer walls are maintained at different constant temperatures $T_1$ and $T_2$ respectively, then

A room has a $4 \mathrm{m}\times 4 \mathrm{m}\times 10 \mathrm{cm}$ concrete roof $\left(k=1.26 \mathrm{w} {\mathrm{m}}^{-1}-{}^{\circ }\mathrm{C}\right)$. At some instant, the temperature outside is $46 °\mathrm{C}$ and that inside is $32 °\mathrm{C}$. If the bricks $\left(k=0.65 \mathrm{w} {\mathrm{m}}^{-1}-{}^{\circ }\mathrm{C}\right)$ of thickness $7.5 \mathrm{cm}$ are laid down on the roof. Calculate the rate of heat flow under the same temperature condition (neglect convection).

A $U$-tube, made of heat- insulating material, is shown in figure. One limb is closed by a non- conducting cork, the temperature is $T_0=300 K$. How much heat (in multiples of $100$ Joule) is required to be given by the coil so that the air rises to a temperature $T=510 K$? The thermal expansion of mercury is negligible. (Take:
Area of the tube as $0.1{ \mathrm{m}}^2,{\rho }_{\mathrm{Hg}}=13.6 \mathrm{g} {\mathrm{cc}}^{-1}; {\mathrm{P}}_{\mathrm{atm}}=75 \mathrm{cm}$ of $Hg,R=\frac{25}{3}$ SI units). Neglect the heat flow through the mercury.

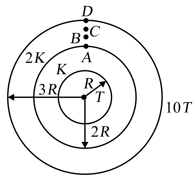
A composite spherical shell is made up of two materials having thermal conductivities $K$ and$2K$  respectively as shown in the figure. The temperature at the inner most surface is maintained at $T$ whereas the temperature at the outer most surface is maintained at $10 \mathrm{T}.\mathrm{A},\mathrm{B},\mathrm{C}$ and $\mathrm{D}$ are four points in the outer material such that $\mathrm{AB}=$ $\mathrm{BC}=\mathrm{CD}$. The net rate of heat flow from the outermost surface to the innermost surface of the shell will be (Neglect any radiation)

The temperature drops through a two-layer furnace wall by $900 °\mathrm{C}$. Each layer is of equal area of cross-section. Which of the following actions will result in lowering the temperature $\theta$ of the interface?

A metal cylinder of mass $0.5\mathrm{kg}$ is heated electrically by a $12\mathrm{W}$ heater in a room at $15°\mathrm{C}$. The cylinder temperature rises uniformly to $25°\mathrm{C}$ in $5\min$ and finally becomes constant at $45°\mathrm{C}$. Assuming Newton's Law of cooling is valid.

Inner surface of a cylindrical shell of length $\ell$ and of material of thermal conductivity $k$ is kept at constant temperature $T_1$ and the outer surface of the cylinder is kept at constant temperature $T_2$ such that $\left(T_1>T_2\right)$ as shown in figure. Heat flows from inner surface to outer surface to outer surface radially outward. Inner and outer radii of the shell are $R$ and $2R$ respectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length $\frac{\ell }{2}$ inner and outer radii $\frac{R}{8}$ and $R$ respectively and thermal conductivity of material $nk$. If rate of radially outward heat flow remains same for same temperature of inner and outer surface i.e. $T_1$ and $T_2$, then find the value of $n$.

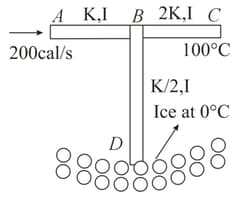
Three rods $AB, BC$ and $BD$ of same length $l$ and cross-sectional area $A$ are arranged as shown. The end $D$ is immersed in ice whose mass is $440 \mathrm{g}$ and is at $0{}^{\circ }\mathrm{C}$. The end $C$ is maintained at $100°\mathrm{C}$. Heat is supplied at constant rate of $200 \mathrm{cal} {\mathrm{s}}^{-1}$. Thermal conductivities of $AB, BC$ and $BD$ are $K, 2K$ and $\frac{K}{2}$, respectively. Time after which whole ice will melt is $\left(K=100 \mathrm{cal}/\mathrm{m}-\mathrm{s}-{}^{\circ }\mathrm{C}, A=10{ \mathrm{cm}}^2, l=1 \mathrm{m}\right)$

One end of the copper rod of uniform cross-section and length $13.5 \mathrm{m}$ is kept in contact with ice and other end with water at $100°\mathrm{C}$. At the distance '$x$' (in meter) from $100°\mathrm{C}$ water along its length a temperature of $400°\mathrm{C}$ is maintained so that in steady-state, the mass of ice melting is equal to that of the steam produced in the same time interval. Write the value of $100x$.

(Assume that the whole system is insulated from its surroundings. Latent heat of fusion of ice and vaporization of water are $80 \mathrm{cal} {\mathrm{g}}^{-1}$ and $540 \mathrm{cal} {\mathrm{g}}^{-1}$, respectively.

If the transmission of heat takes through molecular collisions, it is called

In steady state heat conduction, the equations that determine the heat current $j\left(r\right)$ [heat flowing per unit time per unit area] and temperature $T\left(r\right)$ in space are exactly the same as those governing the electric field $E\left(r\right)$ and electrostatic potential $V\left(r\right)$ with the equivalence given in the table below.

A copper rod of length $2.5 \mathrm{m}$ and an iron rod of length $1.5 \mathrm{m}$ having the same areas of cross section are connected in series. Thermal conductivities of copper and iron are respectively $400$ and $80$ $\mathrm{SI}$ units. The equivalent conductivity of the composite bar in $\mathrm{SI}$ unit is ____.